白话机器学习的数学_读书笔记

2024-09-24#机器学习

0 简介

去图书馆翻阅了很多本深度学习、机器学习、人工智能相关的书籍，但是对我这样从未接触过这一方面的小白来说还是太干涩难懂了。

不过找到了这本很新颖的机器学习讲解书，用对话的形式将复杂公式和底层原理讲得非常清楚，很多公式在之前的书中看了好几遍都没看懂，这本书一两页就讲得很清楚(尤其是梯度下降法)，大赞！

在读这本书之前翻了很多书，跟绫乃有一样的感受，就是不知道要学什么、怎么学。这本书确实给了我拓展了学习这一方面的道路，让我对机器学习有了更好的理解。

1 开始二人之旅

什么是机器学习？

计算机读取大量数据、学习数据的特征并从中找出数据的模式，这样的任务被称为机器学习或模式识别，是从数据中找出特征和模式的技术

机器学习的发展主要归功于具备了能收集和处理大量数据的环境，随着Hadoop、Spark之类的分布式处理技术逐渐成熟，机器学习的应用范围也越来越广，能应用到日常生活、医疗、金融、安全、辅助决策等领域

机器学习的算法

机器学习传统的三项任务：

回归(regression)：处理连续数据（如时间序列数据）使用的技术
分类(classification)：根据已知类别标记的样本来区分未知类别的样本，如第一章中提到的鉴别垃圾邮件（检查邮件内容判断其是否为垃圾邮件），
聚类(clustering)：聚类则是根据数据结构来划分样本中的数据集群，如第一章中提到的摸底考试案例（根据考生考试情况分组得出偏科情况的结论）

分类和聚类的区别在于分类涉及到标签（label），而聚类没有，这引出了有监督学习与无监督学习：

有监督学习：使用有标签的数据进行学习，回归与分类属于有监督学习
无监督学习：使用没有标签的数据进行学习，聚类属于无监督学习

2 学习回归

定义回归模型

现假设有一幅数据图如图1所示。

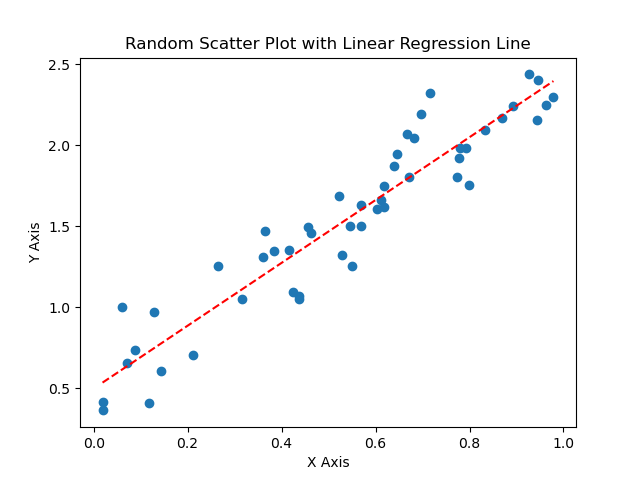
图1 随机数据图

令：

每一个散点对应的 $x$ , $y$ 值分别为 $x^{(i)}$ , $y^{(i)}$
图中的回归曲线为 $f_{\theta}(x)=\theta_0+\theta_1 x$ (一次回归)
散点与回归曲线的误差： $y^{(i)}-f_\theta (x^{(i)})$

理想情况下，我们希望散点能完全落在回归曲线上，因为这样的预测结果最为精确。此时有

$y^{(i)}-f_\theta (x^{(i)})=0$ 但所有误差等于0几乎不可能，于是定义目标函数，即 $n$ 个训练数据的误差之和:

$E(\theta)=\frac{1}{2}\sum^{n}_{i=1}\Big(y^{(i)}-f_\theta (x^{(i)})\Big)^2$

最速下降法(梯度下降法)

最速下降法（梯度下降法）的目的在于不断更新 $\theta$ 的值来减小 $E(\theta)$ ，每次代入数据进去，看其梯度是正还是负，然后沿着梯度的方向进行参数更新。其定义为:

$\theta_0:=\theta_0-\eta\sum^{n}_{i=1}\big(f_\theta(x^{(i)})-y^{(i)}\big)$ $\theta_1:=\theta_1-\eta\sum^{n}_{i=1}\big(f_\theta(x^{(i)})-y^{(i)}\big)x^{(i)}$

多项式回归

用高次项表示更复杂曲线来拟合图像，其表示为：

$f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+…+\theta_nx^n$

多重回归

多重回归是变量超过2个的复杂问题，其表示为：

$f_\theta(x_1,x_2,…,x_n)=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n$

用向量定义有：

$\pmb\theta=\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\\\vdots\\\theta_n\end{bmatrix} \pmb x=\begin{bmatrix}1\\x_1\\x_2\\\vdots\\x_n\end{bmatrix}$

则

$f_\theta(x)=\pmb{\theta}^T\pmb{x}$

梯度下降、随机梯度下降、mini-batch梯度下降

梯度下降法虽然能够一次迭代所有数据的误差进行梯度下降，但计算耗时、容易陷入局部最优解
随机梯度下降在梯度下降的基础上随机抽取一个数据进行梯度下降，不容易陷入目标函数局部最优解，但精度略低
mini-batch梯度下降即抽取一批数据进行梯度下降，结合了梯度下降与随机梯度下降，效果处于两者之间，能较快下降且一定程度避免陷入局部最优，最常用

3 学习分类

主要讨论了感知机与逻辑回归

感知机

我的理解是感知机为神经网络的基本单元

特征（feature）：数据的属性

标签（label）：作为分类数据的标准

训练过程：
1. 随机初始化权重向量进行预测
2. 若判别函数与实际标签不同，则分类结果不正确，需更新 ${w}$ ，通过向量加减来更新方向，使之接近正确方向
3. 若判别函数与实际标签相同，则分类成功
- 判别函数分类失败时才会更新参数值

基本公式为:

$w:=\begin{cases} w+y^{(i)}x^{(i)}~~~~~~~~~~(f_w(x^{(i)})\ne y^{(i)})\\ w~~~~~~~~~~~~~~~~~~~~~~~~~~(f_w(x^{(i)}) =y^{(i)}) \end{cases}$

线性可分

线性可分指能用直线分类，不能用直线分类就不是线性可分
感知机的最大缺点：只能解决线性可分问题

逻辑回归

逻辑回归是将分类以概率角度进行考虑，通过概率预测样本标签实现分类的效果（感觉只要跟“预测”相关就基本上是回归分析）

标签设置以处理方便来自由决定，书中在逻辑回归这一部分将标签分别设定为1与0

Sigmoid函数

函数定义：

$f_\theta(\pmb x)=\frac{1}{1+\text{exp}(-\pmb{\theta}^\text{T}\pmb x)}$

函数图像：

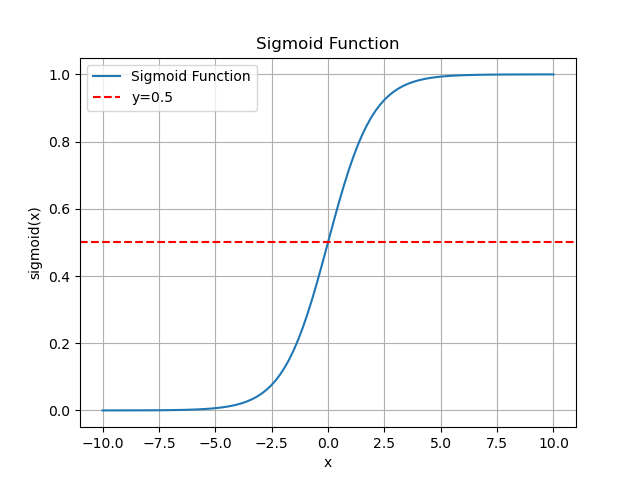
图2 sigmoid函数图像

函数性质：

$0<\sigma(\sdot)<1$
$\sigma(0)=0.5$
$\sigma(\sdot)$ 关于 $(0,0.5)$ 对称

将 $f_\theta(\pmb x)$ 当做概率使用，即

$P(y=1\mid x)=f_\theta(\pmb x)\\$

则标签的更新为：

$y=\begin{cases} 1~~~(f_\theta(\pmb x)\ge 0.5)\\ 0~~~(f_\theta(\pmb x)\lt 0.5) \end{cases}$

此时 $f_\theta(\pmb x)\gt 0.5$ ，有 $\pmb \theta^T\pmb x\gt 0$ ；
反之 $f_\theta(\pmb x)\lt 0.5$ ，有 $\pmb \theta^T\pmb x\lt 0$

\pmb\theta^T\pmb x

就是边界线，即决策边界，以决策边界的两侧来进行分类
那么为了求得正确的决策边界参数的算法就是逻辑回归

似然函数

定义：

$L(\pmb\theta)=\prod^n_{i=1}P(y^{(i)}=1\mid x^{(i)})^{y^{(i)}}P(y^{(i)}=0\mid x^{(i)})^{1-y^{(i)}}$

似然函数 $L(\pmb \theta)$ 越大，越能够最近似地说明训练数据
根据这一条件求出最合适的 $\pmb\theta$

引出对数似然函数,将乘积转化为求和：

$\text{log}L(\pmb\theta)=\text{log}\prod^n_{i=1}P(y^{(i)}=1\mid x^{(i)})^{y^{(i)}}P(y^{(i)}=0\mid x^{(i)})^{1-y^{(i)}}\\~~~~~~~~~~~~~~~=\sum^n_{i=1}\big(y^{(i)}\text{log}f_\theta(\pmb x^{(i)})+(1-y^{(i)})\text{log}(1-f_\theta(\pmb x^{(i)}))\big)$ 参数更新公式：

$\theta_j:=\theta_j-\eta\sum^n_{i=1}\big(f_\theta(\pmb x^{(i)})-y^{(i)})\big)x_j^{(i)}$

参数 $\theta$ 可以通过这样的形式不断更新，从而求出能够使似然函数 $L(\pmb \theta)$ 最大的参数 $\theta$

4 评估

涉及到实际应用机器学习时会出现的问题以及相应的处理方法，包括交叉验证、回归与分类问题的验证、正则化

交叉验证

将一组数据通常分为测试样本和训练样本，其中测试样本一般用于评估模型，大多数采用3:7或者2:8的比例进行随机分配，这样的操作叫做交叉验证

K折交叉验证

把全部训练数据分为K份
将K-1份数据用作训练数据，剩下的1分用作测试数据
每次更换训练数据和测试数据，重复K次交叉验证
最后计算K个精度的平均值，作为最终精度

K折交叉验证非常耗费时间，需要确定一个合适的K值

回归问题的验证

回归是连续值，可以从误差入手
均值方差（MSE,Mean Square Error）:计算测试数据的误差的平方的平均值，公式如下：

$MSE=\frac{1}{n}\sum^{n}_{i=1}\big(y^{(i)}-f_\theta(\pmb x^{(i)})\big)^2$

分类问题的验证

分类需要考虑分类的类别是否正确，采用精确率、召回率、F1值等指标进行评估

以二分类为例，分类是否成功有以下四种情况：

结果标签为正(True)，且分类情况为正(Positive)
结果标签为负(False)，但分类情况为正(Positive)
结果标签为正(True)，但分类情况为(Negative)
结果标签为负(False)，且分类情况为负(Negative)

精度

$Accuracy=\frac{\text{TP+TN}}{\text{TP+FP+TN+FN}}$

精度能掌握分类结果整体的精度，但在遇到极端情况（如某一类数据基本全为负标签）无法评估模型的好坏，于是引入了精确率与召回率

精确率(Precision)：Positive数据所占的比例，公式如下

$Precision=\frac{\text{TP}}{\text{TP+FP}}$

精确率越高，分类错误越少，用于精度检验

召回率(Recall):在Positive数据中，实际被分类为Positive的数据所占的比例

$Recall=\frac{\text{TP}}{\text{TP+FN}}$

召回率越高，说明被正确分类的数据越多

精确率与召回率的分子通常以数量少的那个效果更好

但一般来说，精确率和召回率会一个高一个低，需要进行进一步处理，于是引入F1值

F1值

\pmb {F1}

值用于评定综合性能，在数学上是精确率和召回率的调和平均值，其定义为：

$Fmeasure=\frac{2\sdot Precision \sdot Recall}{Precision+Recall}$

此外还有一个带权重的 $F$ 值指标：

$WeightFmeasure=\frac{(1+\beta^2)\sdot Precision \sdot Recall}{\beta^2 \sdot Precision+Recall}$

正则化

过拟合

过拟合（overfitting）指模型只能拟合训练数据的状态

可以采用以下方法避免过拟合：

增加全部训练数据的质量

个人认为这个方法比较困难，目前在做项目的时候，数据是有限的，但是普遍质量不高
- 使用简单的模型

下文提到的正则化
- 正则化

正则化的方法

回归正则化

在目标函数上添加正则化项，使这个新的目标函数进行最小化，这个方法就是正则化

其中正则化项为：

$R(\pmb{\theta})=\frac{\lambda}{2}\sum^{m}_{j=1}\theta^2_j$

则新的目标函数为：

$E(\pmb{\theta})=\frac{1}{2}\sum^{n}_{i=1}\big(y^{(i)}-f_\theta(\pmb x^{(i)})\big)^2+R(\pmb{\theta})~~~~~~~~~~~~~~~\\=\frac{1}{2}\sum^{n}_{i=1}\big(y^{(i)}-f_\theta(\pmb x^{(i)})\big)^2+\frac{\lambda}{2}\sum^{m}_{j=1}\theta^2_j$

只有参数的项为偏置项 $\pmb{\theta_0}$ ，一般不对它进行正则化
$\lambda$ 是决定正则化项影响程度的正的常数，自己定义

正则化能防止参数变得过大，有助于参数接近较小的值。通过减小不需要的参数的影响，将复杂模型替换为简单模型来防止过拟合

\lambda

则是控制正则化惩罚的强度，若 $\lambda=0$ 就相当于不使用正则化，相反， $\lambda$ 越大，正则化的惩罚越严厉

分类正则化

分类正则化同上，不过目标函数改为了对数似然函数，公式如下：

$\text{log}L(\pmb{\theta})=-\sum^{n}_{i=1}\big(y^{(i)}\text{log}f_\theta(\pmb{x}^{(i)})+(1-y^{(i)})\text{log}(1-f_\theta(x^{(i)}))\big)+\frac{\lambda}{2}\sum^{m}_{j=1}\theta^2_j$

此处注意，目标函数在原来的基础上加上了负号，是因为原来的目标函数以最大化为目标，而现在正则化需要解决最小化问题

上述的正则化为 $\pmb{L2}$ 正则化

L2正则化的参数更新

$\theta_0:=\theta_0-\eta \bigg(\sum^{n}_{i=1}\big(f_\theta(\pmb{x^{(i)}})-y^{(i)}x^{(i)}_j\big)\bigg)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \theta_j:=\theta_j-\eta\bigg(\sum^{n}_{i=1}\big(f_\theta(\pmb{x^{(i)}})-y^{(i)}x^{(i)}_j\big)+\lambda\theta_j\bigg)~~~~~~~~~~(j>0)$

正则化的区别

L1正则化与L2正则化的区别在于他们的正则化项不同

L1正则化项

$R(\pmb \theta)=\lambda\sum^{m}_{i=1}|\theta_i|$

L2正则化项

$R(\pmb{\theta})=\frac{\lambda}{2}\sum^{m}_{j=1}\theta^2_j$

欠拟合

欠拟合是指没有拟合训练数据的状态,出现原因是模型相对于要解决的问题来说太简单了，原因也和过拟合的情况相反

区分过拟合与欠拟合

欠拟合的情况下，随着训练数据的增加，训练数据的精度会下降，如图3所示

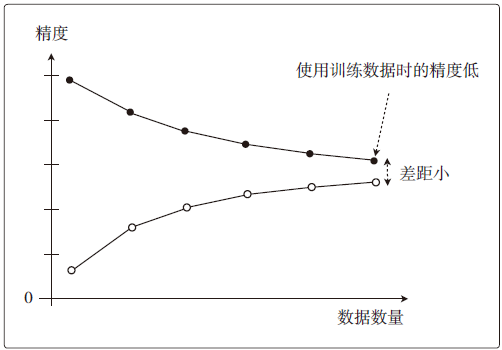
图3 欠拟合学习曲线

图3所示的图像也能被称作高偏差，此时无论使用训练数据还是测试数据，精度都很低

而过拟合的情况下，训练数据的精度一直保持很高的状态，但测试数据的精度一直没有上升到它的水准，如图4所示，这样的情况叫做高方差

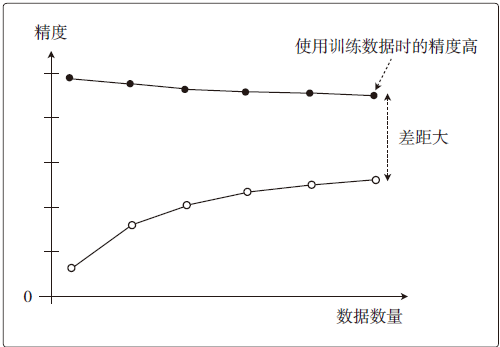
图4 过拟合学习曲线

5 实现

标准化：也可以称为z-score规范化，把训练数据变成平均值为0，方差为1的数据，目的在于使参数收敛速度加快，变化公式如下：

$z^{(i)}=\frac{x^{(i)}-\mu}{\sigma}$

关于这部分我参考书中写了一遍代码进行练习，个人的代码实现参考如下：

learning_part/math_machine_learning at main · Zabwerk/learning_part (github.com)

6 小结

本篇笔记是初探机器学习的第一篇笔记，接下来的计划是阅读《深入浅出图神经网络：GNN原理解析》

本篇笔记参考了大佬Achuan-2的同书笔记，感谢分享！

Zabwerk的元空间